Mathematics

This section is designed to teach you a little bit of linear algebra because it will be used in our computer a lot. Linear algebra is crucial to both polarization and quantum physics so we will focus on that mainly. NOTE: If you have taken any linear algebra class this should be completely unnecessary so feel free to skip it

This section will include:

Vectors
Vector operations
Matrices
Tensor product
Bloch sphere

Vectors

To explain everything behind quantum computing and generally anything quantum related, basic knowledge of linear algebra is absolutely req. That is why in this section we’ll be briefly explaining most of the basic principles of linear algebra as a refresh. We suggest you learn proper linear algebra in order to continue (here and here)

Vectors are the heart and soul of linear algebra and the most important geometric object when trying to describe qubits. To first understand vectors, we need to define and separate scalars from vectors.

Scalar is a quantity having only magnitude and no direction. If only α is a Real number

Vector is a quantity with both magnitude and direction. They are symbolized with an arrow across the top

\[\vec{u}\]

Where n the number of dimensions in a mathematical space. Examples:

\[\alpha \in \mathbb{R}^n\]

\[\begin{split}u \in \mathbb{R}^2 : \vec{u} = \begin{pmatrix} x \\ y \end{pmatrix}\end{split}\]

\[\begin{split}U \in \mathbb{R}^3 : \vec{U} = \begin{pmatrix} x \\ y \\ z \end{pmatrix}\end{split}\]

Vector magnitude describes the length of the vector:

\[\| \vec{u} \| = \sqrt{x^2 + y^2}\]

Vector direction shows the direction the vector is pointing:

\[\tan \theta = \frac{ y }{ x }, x \ne 0\]

Vector operations

Now we will very briefly go over a few of the vector operations which will be very useful in our computations later. If you don’t feel very comfortable with these concepts we suggest that you practice before continuing this is meant more as a refresh.

Vector addition

\[\begin{split}\vec{\alpha} + \vec{\beta} = \left[ {\begin{array}{cc} x_{\alpha} + x_{\beta} \\ y_{\beta} + y_{\beta} \\ \end{array} } \right]\end{split}\]

Vector subsection

\[\begin{split}\vec{\alpha} + (-\vec{\beta}) = \left[ {\begin{array}{cc} x_{\alpha} - x_{-\beta} \\ y_{\beta} - y_{-\beta} \\ \end{array} } \right]\end{split}\]

Scalar-Vector Multiplication

\[\begin{split}\phi \cdot \vec{\alpha} = \left[ {\begin{array}{cc} \phi \cdot x \\ \phi \cdot y \\ \end{array} } \right]\end{split}\]

Inner product

We define inner product is the operation between 2 non-zero vectors and that always gives a scalar result. It can be symbolized as:

\[\vec{\alpha} \cdot \vec{\beta} = x_{\vec{\alpha}} \cdot x_{\vec{\beta}} + y_{\vec{\alpha}} \cdot y_{\vec{\beta}}\]

Inner product can be used as a tool for calculating the magnitude:

\[\langle\vec{u},\vec{u}\rangle = \vec{u} \cdot \vec{u}\dagger = \sum\limits_{i = 1}^n {u_1 \cdot u_1} = \sum\limits_{i = 1}^n = {\| \vec{u} \|}^2\]

Or for vector normalization:

\[\frac{\vec{u}}{\sqrt{\langle\vec{u} , \vec{u}\rangle}} = \frac{\vec{u}}{\|\vec{u}\|}\]

Matrices

Matrices are rectangular arrays of numbers, symbols and expressions arranged in columns and rows, used to to mathematically describe objects such as quantum gates. For example:

\[\begin{split}\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}\end{split}\]

That is a matrix called “2x3 matrix” because it consists of 2 rows and 3 columns. A matrix is called unitary when its conjugate transpose is also its inverse.

Tensor product

Tensor product the only matrix operation we really recommend that you get very familiar with it since it’s used a lot in quantum computing. We will simply offer a refresh here but you can read more here

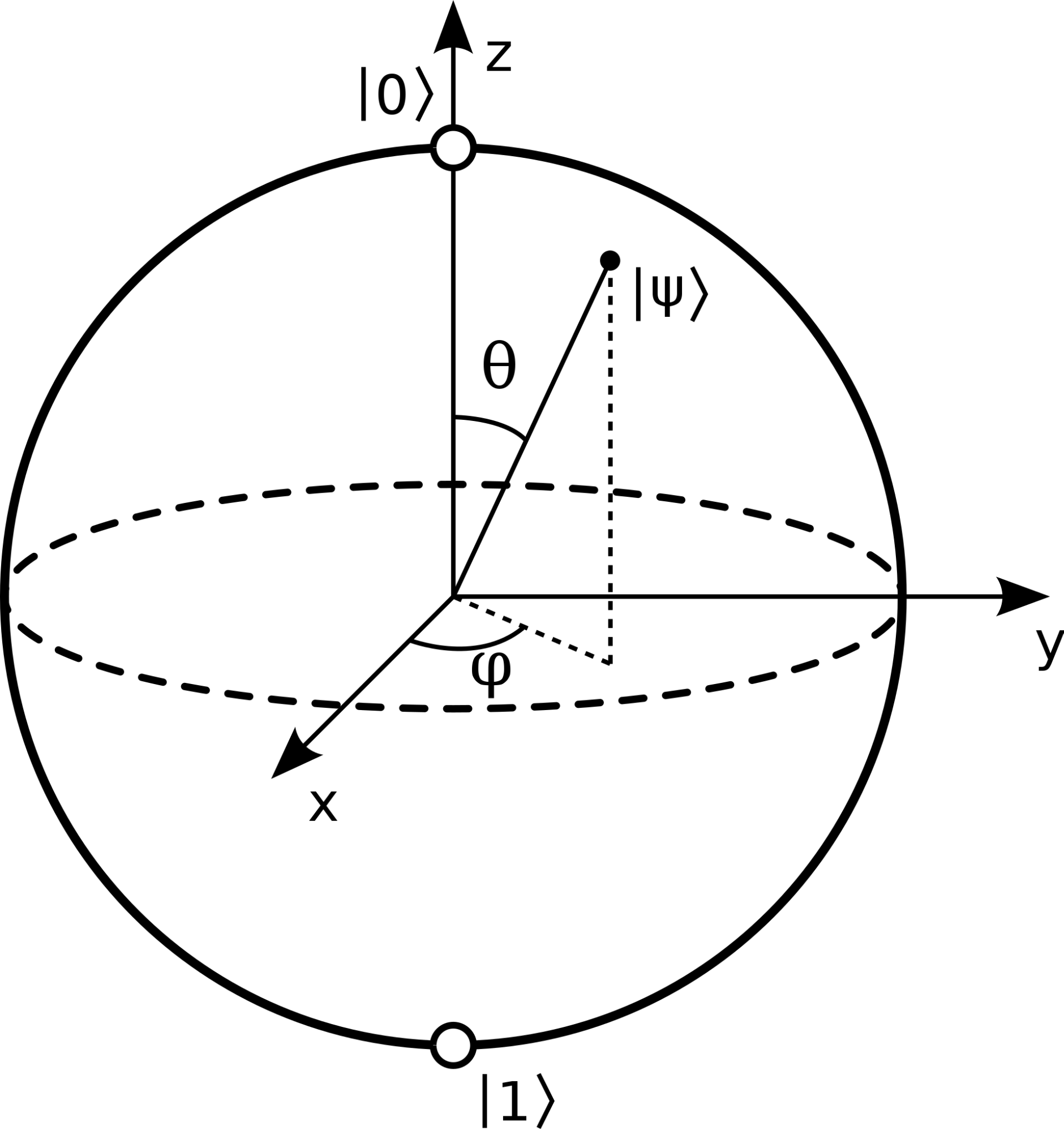
\[\begin{split}\begin{pmatrix} \alpha \\ \beta \end{pmatrix} \otimes \begin{pmatrix} \gamma \\ \delta \end{pmatrix} = \begin{pmatrix} \alpha \cdot \begin{pmatrix} \gamma \\ \delta \end{pmatrix} \\ \beta \cdot \begin{pmatrix} \gamma \\ \delta \end{pmatrix} \end{pmatrix} = \begin{pmatrix} \alpha \cdot \gamma \\ \alpha \cdot \delta \\ \beta \cdot \gamma \\ \beta \cdot \delta \end{pmatrix}\end{split}\]

Bloch sphere

The Bloch sphere (named after Felix Bloch) is one of the most fundamental concepts of quantum computing. In essence, the Bloch sphere is a geometrical representation of the pure state space of a qubit. In the poles of the sphere we have the 2 states of our qubit and a vector representing the state of the system. Basically, it is a unit sphere used to visualize the probability data we get from measuring our computer. IMPORTANT: The bloch sphere is a 2D hilbert space and not a 3D space as the name sphere may suggest.